RASTGELE SAYILAR ÜZERİNE
RASTGELE SAYILAR ÜZERİNE
Rastgele sayı üretimi şansa bırakılamayacak kadar önemlidir.
Robert R. Coveyou
İnternetten rand() yadan random() diye arattığınızda karşınıza şu tarz örnekler çıkacaktır.
#include <stdio.h>
#include <stdlib.h>
int main()
{
int random;
random = rand();
printf("%d", random);
return 0;
}
İsimlerine baktığımızda rastegele sayılar ürettiklerini iddia eden bu fonksiyonlar acaba gerçekten de rastgele sayılar mı üretiyorlar? Aslında cevap 'hayır'. Rastgele sayı üretmiyorlar. Bunu anlamak için önce rastgelelik nedir bunu incelemek gerekiyor.
Rasgelelik
Rastgelelik anlaşılması zor bir konu. İspatlanması ise imkansız. Şöyle bir örneğe bakalım.

00000 sayısını incelersek bu bir rastgele bir sayı mıdır? Yoksa değil mi? Bir rastgele sayı üreteci doğal bir şekilde bu sayıyı üretebilir. Ardarda 2 defa 0 geldiğinde şüphelenmeyiz. Çünkü bu gayet doğaldır. Ardarda iki defa 0 gelebilir. Ardarda 3 defa da gelebilir. Ardarda 5 defa da gelebilir. Bu gayet normaldir. Ardarda 100 defa 0 da gelebilir. Bu da hala bir rastgele sayıdır. Bu durumun gerçekleşme ihtimali ise 1/(10)^100 dür. Yine de bir rastgele sayı.
İşin özünü ise bu oluşturuyor. Bir sayının yada sayı dizisinin rastgele olup olmadığını ispatlamak yada inkar etmek zordur. Hatta imkansız. Bu da bizi kaçınılmaz bir belirsizliğe görütüyor.
Rastgele sayı üretimi zor bir problem. Çözümü de aynı şekilde zor. Rastgele sayı üretimi için bir çok yöntem geliştirildi, birçok teori üretildi, donanımlar geliştirildi, yazılımlar üretildi. Peki buna ne gerek var? Yani gerçekten gerek var mı?
Kullanım alanları
Rastgele sayılar ve rastgele sayı üreteçleri rastgeleliğe ihtiyaç duyulan her yerde kullanılır. Şans oyunları, istatistiksel örneklemeler, bilgisayar oyunları, kumar oyunları, kriptografi, tahmin edilemeyen sonuçlar üreten her alanda geniş bir kullanım alanına sahiptir.
Bir oyun oynarken rastgele cereyan eden olayların gerçekten rastgele olması beklenir veya bir simülasyonda verilerin rastgele olması önemlidir.
Bilgisayar biliminde rastgele sayıların en önemli kullanım alanlarından biri de kriptoloji ve şifreleme işlemleridir. Rastgele sayılar şifreleme işleminin gizliliği ve güvenilirliği açısından oldukça önemlidir. Şifreleme işleminde kullanılacak sayının belirli bir düzene bağlı olması veya tahmin edilebilir, rastgelelikten uzak olması şifrenin kırılmasını oldukça kolaylaştıracaktır.
Şans Oyunları
Bir kart oyunu düşünün. Oyun başında veya herhangi bir yerinde kartlar dağıtılırken bu işlemin rastgele olmasını bekleriz. Belirli bir kurala göre dağıtılmasını hiç kimse istemez.
Daha kötüsü belirli bir kurala göre dağıtıldığı düşünülürse bu hile yapmak isteyenler için bir fırsat oluşturacaktır.
Bu nedenlerden dolayı burada gerçekten rastgele sayı üretimine ihtiyaç vardır.
Bilgisayar Oyunları
Herhangi bir bilgisayar oyunu oynarken yaptığınız saldırı gücü, ödül olarak aldığınız bir kutunun açılması vb. durumlarda rastgele sayılara ihtiyaç duyulur.
Belirli bir kural burada kullanılmamalıdır. Çünkü belirli bir kural kullanılması ve bu kuralın başka bir kişi tarafından keşfedilmesi ile keşfeden o kişi bunu kendi lehine kullanabilir.
Kriptografi
Kriptorafiyi rastgele sayıların kullanıldığı en kritik alan olarak değerlendirebiliriz. Nedeni ise güvenlik.
Söz konusu güvenlik olunca bu noktada hataya yer verilmiyor. Bir bankanın web uygulaması üzerinden işlem yaparken kuallınılan şifreleme anahtarının rastgele sayılar kullanılarak üretilmemesi bir felakete yok açabilir. Ya da bir telefon konuşması yaparken kullanılan anahtar güçlü olmalıdır. Bu da rastgele sayılar ile mümkün olabilir.
Bir örnek vermek gerekirse c dili ile rastgele sayı üretmek için şuna benzer bir kod olduğunu düşünelim.
#include <stdio.h>
#include <stdlib.h>
#include<time.h>
int main()
{
int random;
srand(time(0));
random = rand();
printf("%d", random);
return 0;
}
Bu kod bloğu o anki saniyeyi tohum olarak kullanarak rastgele sayı üretiyor. Fakat saniyede binlerce işlem yapabilen bir bilgisayar bu kod bloğu ile aynı saniyede binlerce kez aynı rastgele sayıyı üretecektir. Bu kod bloğunu kriptografik bir işlemde kullandığımızı düşünelim. Bir sunucuda şifreleme için anahtar üretim algoritmasının içinde uygulandığını varsayarsak şöyle bir felaket olacaktır. Aynı saniye için oluşturulan bütün anaytarlar aynı olacaktır ve şifreleme işlemi aynı anahtar ile yapılacaktır. Bu güvenlik açısından bir felakettir.
Şimdi buna bir kaç örnek verelim.
https
Öncelikle https nedir? Wikipedia'daki tanıma bakalım
HTTPS (HTTP Secure, Türkçe güvenli hiper metin aktarım iletişim protokolü) bir bilgisayar ağı üzerinden güvenli iletişim için internet üzerinde yaygın olarak kullanılan bir HTTP( hiper metin aktarım iletişim protokolü) uzantısıdır. HTTPS'te, iletişim protokolü Taşıma Katmanı Güvenliği (TLS) veya öncesinde, onun öncülü/selefi olan Güvenli Soket Katmanı (SSL) ile şifrelenir. Bu nedenle protokol sık sık HTTP üzerinden TLS veya HTTP üzerinden SSL olarak da adlandırılır. [1]
Https internet üzerinde en çok kullanılan protokoldür. Aynı zamanda güvenli bir iletişimi vaad eden bir protokoldür.
Https ile ilk defa iletişim kurarken güvenli bir bağlantı için şifreleme anahtarı belirlenmelidir. Bu anahtar belirlenirken rastgele sayılar kullanılır.
Web tarayıcınız sunucu sertifikasını doğruladıktan sonra şifreleme anahtarını belirler. İşte tam bu noktada rastgele sayılara ihtiyaç duyulur. Rastgeler sayılar kullanılarak şifreleme anahtarı üretilir ve sunucu sertifikasınfaki public key ile şifrelenerek sunucuya iletilir. Bu andan itibaren rastgele sayılar kullanılarak üretilen şifreleme anahtarı simetrik bir şifrelemede kullanılarak güvenli iletişim başlar.
Dikkatinizi rastgele sayı üretimine çekmek isterim. Bu şifreleme işlemindeki güvenlik kritik ölçüde üretilen sayılara bağlıdır. Aksi takdirde gizli kalması gereken iletişim açığa çıkabilir.
ssh
Öncelikle ssh protokolünün wikipediadaki tanımına bakalım:
Güvenli Kabuk (SSH), ağ hizmetlerinin güvenli olmayan bir ağ üzerinde güvenli şekilde çalıştırılması için kullanılan bir kriptografik ağ protokolüdür. En iyi bilinen örnek uygulaması bilgisayar sistemlerine uzaktan oturum açmak için olandır.
Ssh protokolü uzaktaki bir bilgisayarda güvensiz bir ağ üzerinden güvenli bir şekilde iletişim kurmak için kullanılan en yaygın protokoldür. Bu ssh protokolünü ve o protokolün güvenliğini kritik bir öneme sahiptir.
Ssh ile ileltişim başlarken Diffie-Hellman anahtar değişim protokolü ile şifreleme anahtarı üretilir. Bu anahtar üretimi sırasında rastgele sayılardan faydalanılır.
Anahtar değişimi sırasında her iki taraf (sunucu ve istemci) rastgele sayılar üretirler. Ve bu rastgele sayılar ile anahtar değişimi yapılır. Yani buradaki güvenlik üretilen rastgele sayılara bağlıdır.
Web uygulamaları Session Anahtarları
Bir web uygulamasına girdiğinizde web uygulamasının cookie ile tarayıcıya bir key atadığını görürsünüz. Bu uygulama bir php uygulaması ise 'PHPSESSID' ismi ile atanacaktır. (Diğer programlama dilleri yada platformlar için bu değişebilir.) Bu değer rastgele sayı üreteçleri ile üretilmiştir. Rastgele sayı kullanılmasındaki amaç sonraki yada önceki üretilen anahtarların bulunmasını engellemektir. Eğer bir anahtar ile diğerleri bulunabilir olsaydı bu durum güvenlik açısınran bir felakete neden olurdu.
Önemi
Rastgele sayılar güvenlik açısından kritik öneme sahiptir. Birçok protokolde şifreleme anahtarları rastgele sayılar kullanılarak üretilir. Bu da rastgele sayı üretiminin ne kadar önemli olduğunu bize gösteriyor.
Burayı anlamak için daha önce yaşanan bir olayı inceleyelim.
Debian Linux dağıtımı, sunucu ve masaüstü dünyasında en popüler Linux dağıtımlarından biri. Ubuntu, Mint gibi popüler dağıtımlar Debian dağıtımdan türetiliyorlar. [2]
C programlama dili yapısal olarak güvenlik açısından ciddi problemlere sahiptir. Bu problemleri azaltmak için C kodlarını tarayan ve riskli kod parçalarını bulmaya çalışan çeşitli programlar kullanılıyor. Debian geliştiricileri libssl şifreleme kütüphanesini taradılar ve kimi zafiyetler tespit ettiler.
Geliştiricilerin arasındaki bu kou hakkındaki tartışmaları okumak hala mümkün. Özetle "ne yapacağız bu kod hata veriyor.", "Bu satırlar hata veriyor silsek mi acaba?" gibi konuşmalar geliştiriciler arasında geçiyor. Debianın hata yönetim sisteminden bir alıntı: [3]
The problems are the following 2 pieces of code in
crypto/rand/md_rand.c:
247:
MD_Update(&m,buf,j);
467:
#ifndef PURIFY
MD_Update(&m,buf,j); /* purify complains */
#endif
What it's doing is adding uninitialised numbers to the pool to
create random numbers.
I've been thinking about commenting those out.
I've been told that using VALGRIND_MAKE_READABLE can be used to
suppress those errors. So I've been pondering about building the
library with that. I haven't tried that this works yet though.
Martin, what do you think about this?
Bu satırlar “geliyorum” diyen bir felaketin habercileri. O kritik, “sorunlu” kod satırı silindi. Bu 2006 yılında oldu.
Sonuç itibarıyla libssl’de kritik bir işleme giren entropi 16 bitlik bir seviyeye düştü.
Bunun sonuçlarını anlamak için kullanılan kriptografinin nasıl çalıştığını kısaca anlatmak gerek. RSA açık anahtarlı şifreleme teknolojisi büyük (hem de çok büyük) asal sayıları kullanıyor. Kriptografik sır iki büyük asal sayı, size mesaj göndermek isteyen kişiler ile paylaştığınız public (genel) anahtarınız bu iki sayının çarpımından üretiliyor.
Dolayısıyla asal sayıları bulmak mümkün olunca kriptografik yöntemin sırrı açıklanmış oluyor.
Sorun, sürece giren entropi sadece 16 bitlik ise, üretilen büyük asal sayılar sadece 65.535 asal sayı içeren bir havuzdan seçiliyor. Bilgisayarlar hızlı çalışıyor; iyilik için de kötülük için de. Bir saldırgan birkaç milisaniye içinde 65 bin olası anahtarı deneyip kapıdan içeriye geçebiliyor.
Maalesef aynen tarif ettiğimiz şekilde oldu. Bu kod satırının silinmesiyle, Debian ve türevlerinin son versiyonunu yükleyen her sunucunun kapısı çok basit saldırı programlarına açıldı. Sorun ancak 2008 yılında tespit edildi. Yani 2 yıl boyunca bu güvenlik açığı kullanılmaya devam etti [2].
Rastgele Sayı Üreteçleri
Bilgisayarlar son derece deterministik makinalardır. Aynı girdi için her zaman aynı çıktıyı verirler. Hal böyle olunca bilgisayarlarda rastgele sayı üretmek oldukça güç bir hal alıyor.
Bilgisayarlarda rastgele sayı üretmek için pek çok yöntem geliştirildi. Bu yöntemleri genel olarak iki kategoriye ayırabiliriz. Bunlar şu şekildedir.
- Sözde Rastgele Sayı Üreteçleri
- Gerçek Rastgele Sayı Üreteçleri
Bu kategorileri detaylı bir şekilde inceleyelim.
Sözde Rastgele Sayı Üreteçleri (Pseudo-Random Number Generators PRNG)
Bu üreteçler bir başlangıç değeri ile rastgele sayı üretirler! Rastgele ile kastımız rastgele gibi görünen sayılar üretirler.
Sözde rastgele sayı üreteçleri bir ilk değer ile başlarlar. Daha sonra yeni bir rastgele sayı istendiğinde bir önceki sayı bir algoritma içerisinde kullanılarak yeni bir rastgele sayı üretilir.
Örneğin bir sözde rastgele sayı üreteci bir önceki sayının karesini alarak üretilen bu sayının bazı basamaklarını alarak yeni bir sözde rastgele sayı üretebilir.
Bu noktada farklı algoritmalar kullanılabilir. Algoritma ne kadar karışık olursa üretilecek sözde rastgele sayılar o oranda entropisi yüksek sayılar olacaktır.
Bu noktada üretilen rastgele sayılar ve rastgele sayılar dizisi ile verilen sayıya bağlıdır. Bu ilk sayı çekirdek değer (seed - tohum) olarak adlandırılır. Bu sayı değiştikçe üretilen sayılar da değişecektir. Aynı seed verildiği sürece aynı sayılar üretilecektir. Bu yüzden bu tip sayı üreteçlerine sözde (pseudo) sayı üreteçleri denir.
Sözde rastgele sayı üreteçlerinde amaç hızlı ve rastgele görünümlü sayı üretmektir. Hızlı olması önemlidir çünkü günümüz programları ve yazılımları çok hızlı çalışırlar. Aynı şekilde çok fazla rastgele sayıya ihtiyaç duyarlar.
Aynı şekilde güvenliğin kritik olmadığı sistemlerde rastgele sayı üretimi maliyetinin düşmesi ve hızlı çalışması için sözde rastgele sayı üreteçleri tercih edilebilir.
Sözde rastgele sayı üreteçleri için diğer bir önemli özellik periyotlarının uzun olmasıdır. SRYÜ bir algoritma ve tohum ile sayı ürettikleri için belirli bir sayıdan sonra tekrar etmeye başlayacaklardır. Örnek vermek gerekirse tohum olarak 2 haneli bir sayı kullanılırsa SRSÜ en fazla 100 rastgele sayı üretecektir. Yani belli bir miktar sayı üretiminden sonra tekrar tohum değerine dönecektir. İşte başlangıç noktası olan tohum değerinden tekrar aynı tohum değerinin üretilmesi arasındaki geçen zamana periyot deriz.
Periyot uzunluğunun fazla olması sözde rastgele sayı üreteçleri için oldukça önemlidir ve mümkün olduğunca büyük bir değer olması gerekir. Aksi takdirde sondaki üretilecek sayının kestirilme ihtimali ortaya çıkacaktır.
Periyodu etkileyen diğer bir önemli husus ise kullanılan algoritmadır. Basit algoritmalar periyot değerine kısa sürede ulaşırlar. Karmaşık algoritmaların ise periotlarına ulaşmaları daha uzun sürer. Bu yüzden kullanılan algoritma olabildiğince karışık olmalıdır.
Gerçek Rastgele Sayı Üreteçleri (True-Random Number Generators TRNG)
Gerçek rastgele sayı üreteçleri dış bir kaynaktan girdi alarak sayı üreten üreteçlerdir. Gerçek rastgele sayı üreteçlerini gerçekten rastgele yapan şey rassallığın fiziki/dış dünyadan gelmesidir. Ve herhangi bir algoritma kullanılmadığı için sonraki üretilen sayının ne olacağının kestirilemez olmasıdır.
Burada rastgele sayı üretimi için dış dünyadan veri alınmasının nedeni ise dış dünyanın deterministik olmamasıdır. Yani dış dünyanın bir zaman diliminde nasıl davranacağı tam olarak kestirilemez. Bu sayede bilgisayarlardaki deterministik yapı aşılmış olacaktır.
Burada kullanılan fiziki/dış etki pek çok şey olabilir. Bunlardan bazılarını şu şekilde listeleyebiliriz.
- Atmosferik ölçüm
- Sıcaklık
- Fave ve klavye hareketleri
- Radyoaktif değişimler
- Elektromanyetik ölçüm
Yukarıdaki gibi ortamlardan çok hassas ölçümler alınarak ile rastgele sayılar üretilir. Ölçümler çok çok hassas olduğu için bir önceki üretilen rastgele sayı bilinse dahi sonraki sayının ne olacağı bilinemez.
Örnek olarak bir insanın fare hareketinde bir anki hareket değeri çok hassas bir ölçümle alınabilir. İnsan deterministik olmadığı için aynı hızda ve aynı açı ile fareyi tekrar hareket ettirmesi çok olası değildir. Bu nedenle fare hareketleri girdi olarak alındığında gerçek rastgele sayı üretilebilir.
Gerçek rastgele sayı üreteçleri güvenliğin kritik öneme sahip olduğu alanlarda oldukça yaygın olarak kullanılır.
Gerçek rastgele sayı üreteçlerinin de kendine ait bazı sorunları vardır.
Gerçek manada rastgele sayı ürettikleri için maliyetlidirler. Hem zaman hemde parasal olarak kullanılmaları ve gerçeklenmeleri zordur. Bir örnek vermek gerekirse c ve rand() fonksiyonu ile saniyede binlerce sözde rastgele sayı üretilebilir. Fakat gpg gibi gerçek rastgele sayı üreten uygulamaların sayıyı üretmesi birkaç saniye alacaktır.
Donanım tabanlı çalıştıkları için kullanılan donanımın yanlış konfigüre edilmesi oldukça kolaydır. Ayrıca kullanılan donanım belli etmeden (sessizce) bozulabilir. Bir örnek vermek gerekirse, radyoaktivite ile rastgele sayı üreten cihazlar verilebilir. Bu tür cihazlardaki hata çeşitleri oldukça fazla, karmaşık ve tespit edilmeleri ise oldukça zordur.
Birçok entropi kaynağı genellikle oldukça kırılgan ve belli etmeden bozulduğu için, bu entropiler üzerinde sürekli olarak verdikleri çıktıları takip eden istatistiksel testler gerçekleştirilmelidir. Bu tür cihazların çoğunluğu, yazılım içerisinde cihazı okuyan testler içermektedir. [9]
Rastgele Sayı üreteci Testleri
Rastgele sayılar ve rastgele sayı üreteçleri kritik öneme sahiptir. Bu yüzden dolayı rastgele sayı üreteçlerinin doğdu bir şekilde çalıştığından emin olunmalıdır. Bu bölümde rastgele sayı üreteçleri üzerine uygulanan testlerden bahsedilecektir.
Rastele sayı üreteçleri ve üretilen sayılar iyi istatistiksel özelliklere sahip olmalıdırlar. Rastgele sayıların istatistiksel özelliklerini belirlemek için NIST, Diehand ve FIPS gibi test setleri vardır.
NIST testleri
NIST test suitinde toplam 15 test mevcuttur. Üretilen rasgele sayılar bu testlerin tümünden başarılı olmak zorundadır.
Sayıların testlerden başarılı olması için iki önemli parametre vardır. Bunlar önem seviyesi (α) ve Pvalue’dir. Önem seviyesinin 0.01 olarak seçilmesi test edilecek sayıların rasgeleliğinin 99% güven değerine sahip olduğunu belirtir. Rasgelelik ölçüsü olarak hesaplanması gereken P-value 1’e eşit olursa sayılar mükemmel rasgeleliğe sahiptir denir. Aksi durumda sayıların rasgele olmadığı kabul edilir.[4]
Şimdi bu 15 testi biraz yakından inceleyelim.
1. Frequency (Monobits) Test
Testin odağı, tüm dizi için sıfır ve birlerin oranıdır. Bu testin amacı, bir sekanstaki birlerin ve sıfırların sayısının, gerçekten rastgele bir sekans için beklenenden yaklaşık olarak aynı olup olmadığını belirlemektir. Test, fraksiyonlarının 1/2 ye yakınlığını, yani bir sekanstaki sıfır ve birlerin sayısını yaklaşık olarak aynı olmasıdır.
2. Test For Frequency Within A Block
Testin odak noktası, M bitlik blokların içindeki sıfırların ve birlerin oranıdır. Bu testin amacı, bunların frekansının bir M-bit blok olup olmadığını yaklaşık M / 2 olup olmadığını belirlemektir.
Bu testin amacı, bir M-bit bloktaki sıfırların oranının yaklaşık olarak M/2 ve birlerin oranının yaklaşık olarak M/2 olup olmadığını test etmektir.
3. Runs Test
Bu test bit dizisindeki akışların toplam sayısıyla ilgilidir. Akış ardışık aynı bit sıralamasını ifade eder. Böylece 0’lar ve 1’ler arasındaki dalgalanmaların kontrolü sağlanarak üretilen bit dizisinin yavaş ya da hızlı olabileceği konusunda fikir verir [10]
Çalışma testinin amacı, çeşitli uzunluklardaki uzunluk ve sıfırların çalışma sayısının rastgele bir dizi için beklendiği gibi olup olmadığını belirlemektir. Özellikle, bu test, bu alt dizeler arasındaki salınımın çok hızlı mı yoksa çok yavaş mı olduğunu belirler.
4. Test For The Longest Run Of Ones In A Block
Testin odağı, M-bit bloklar içinde en uzun süren birlerdir.
Bu testin amacı, test edilen sekans içindeki en uzun birlerin uzunluğunun, rastgele bir sekansta beklenebilecek en uzun birlerin uzunluğuyla tutarlı olup olmadığını belirlemektir. En uzun olanların beklenen uzunluğundaki düzensizliğin, en uzun sıfırın beklenen uzunluğundaki beklenen düzensizliğin de olduğunu ima ettiğini unutmayın.
5. Random Binary Matrix Rank Test
Testin odağı, tüm dizinin ayrık alt matrislerinin sırasıdır.
Bu testin amacı, orijinal dizinin sabit uzunluklu alt dizileri arasında doğrusal bağımlılığı kontrol etmektir
6. Discrete Fourier Transform (Spectral) Test
Bu testin odak noktası, ayrık Hızlı Fourier Dönüşümü'nün tepe yüksekliğidir.
Bu testin amacı, test edilen sırada rastgele özellik varsayımından sapmayı gösterecek periyodik özellikleri (yani, birbirine yakın olan tekrar eden desenler) tespit etmektir.
7. Non-Overlapping (Aperiodic) Template Matching Test
Bu testin odak noktası, önceden tanımlanmış hedef alt dizelerin gerçekleşme sayısıdır.
Bu testin amacı, belirli bir periyodik olmayan (aperiodic) paternin çok fazla oluşumunu gösteren sekansları reddetmektir. Bu sınama ve Çakışan Şablon Eşleştirme sınaması için, belirli bir m-bit kalıbını aramak için bir m-bit penceresi kullanılır. Desen bulunamazsa, pencere bir bit konumu kayar. Bu test için, kalıp bulunduğunda, pencere bulunan kalıptan sonraki bitine sıfırlanır ve arama kaldığı yerden devam eder.
8. Overlapping (Periodic) Template Matching Test
Bu testin odak noktası, önceden tanımlanmış hedef alt dizelerin sayısıdır.
9. Maurer's Universal Statistical Test
Bu testin odak noktası, eşleşen modeller arasındaki bit sayısıdır.
Testin amacı, dizinin bilgi kaybı olmadan önemli ölçüde sıkıştırılıp sıkıştırılamayacağını tespit etmektir. Aşırı sıkıştırılabilir bir dizinin rastgele olmadığı kabul edilir.
10. Linear Complexity Test
Bu testin odak noktası, üreten bir geri besleme kaydının uzunluğudur.
Bu testin amacı, dizinin rastgele kabul edilecek kadar karmaşık olup olmadığını belirlemektir. Rastgele diziler daha uzun bir geri besleme yazmacı ile karakterize edilir. Kısa bir geri bildirim kaydı, rasgele olmama anlamına gelir.
11. Serial Test
Bu testin odak noktası, tüm sekans boyunca çakışan her bir m-bit paterninin frekansıdır.
Bu testin amacı, 2m m-bit çakışan örüntülerin meydana gelme sayısının, rastgele bir sekans için beklenenden yaklaşık olarak aynı olup olmadığını belirlemektir.
12. Approximate Entropy Test
Bu testin odak noktası, çakışan her bir m-bit paterninin frekansıdır.
Testin amacı, birbirini izleyen/bitişik iki uzunluktaki (m ve m + 1) üst üste binen blokların sıklığını rastgele bir dizi için beklenen sonuçla karşılaştırmaktır.
13. Cumulative Sum (Cusum) Test
Testin amacı, test edilen sekansta meydana gelen kısmi sekansların kümülatif toplamının, rasgele sekanslar için bu kümülatif toplamın beklenen davranışına göre çok büyük veya çok küçük olup olmadığını belirlemektir.
Bu kümülatif toplam rastgele bir yürüyüş olarak düşünülebilir. Rastgele bir dizi için, rastgele yürüme sıfıra yakın olmalıdır. Rastgele olmayan diziler için, bu rastgele yürüyüşün sıfırdan uzaklaşmaları çok büyük olacaktır.
14. Random Excursions Test
Bu testin amacı, rastgele bir yürüyüş içindeki bir duruma yapılan ziyaret sayısının rastgele bir sekans için beklenenden fazla olup olmadığını belirlemektir.
15. Random Excursions Variant Test
Bu testin odağı, belirli bir durumun kümülatif toplam rasgele yürüyüşte gerçekleşme sayısıdır.
Bu testin amacı, rasgele yürüyüşte çeşitli durumların beklenen oluşum sayısından sapmaları tespit etmektir.
Diehard Testleri
Diehard testleri rasgele sayı üretecinin kalitesini ölçmek için kullanılan istatistiksel testlerden oluşan bir test setidir. George Marsaglia tarafından birkaç yıl içinde geliştirildi ve ilk olarak 1995'te yayınlandı.
1. Birthday spacings
Geniş aralıklarla rastgele noktalar seçin. Noktalar arasındaki boşluklar asimptotik olarak üstel olarak dağıtılmalıdır. Adı doğum günü paradoksuna dayanmaktadır.
2. Overlapping permutations
Ardışık beş rasgele sayının dizilerini analiz edin. 120 olası sıralama, istatistiksel olarak eşit olasılıkla gerçekleşmelidir.
3. Ranks of matrices
{0,1} üzerinde bir matris oluşturmak için bazı rastgele sayılardan bir kaç bit seçin, ardından matrisin sırasını belirleyin. Rütbeleri sayın.
4. Monkey tests
Bazı bitlerin dizilerini "kelimeler" olarak kabul edin. Bir akıştaki çakışan kelimeleri sayın. Görünmeyen "kelime" sayısının bilinen bir dağılımı izlemesi gerekir. İsim sonsuz maymun teoremine dayanmaktadır.
5. Count the 1s
Ardışık veya seçilen baytların her birinde 1 bit sayın. Sayıları "harflere" dönüştürün ve beş harfli "kelimelerin" oluşumlarını sayın.
6. Parking lot test
Birim dairelerini rastgele bir 100 × 100 kareye yerleştirin. Bir çevre, başarılı bir şekilde park edilmiş bir daireyle çakışmazsa başarıyla park edilir. 12.000 denemeden sonra, başarılı bir şekilde park edilmiş çevrelerin sayısı belirli bir normal dağılımı izlemelidir.
7. Minimum distance test
Rastgele 8000 noktayı 10000 × 10000 kareye yerleştirin, ardından çiftler arasındaki minimum mesafeyi bulun. Bu mesafenin karesi belli bir ortalama ile katlanarak dağıtılmalıdır.
8. Random spheres test
1000 kenarındaki bir küpte rastgele 4000 nokta seçin. Yarıçapı başka bir noktaya olan minimum mesafe olan her noktayı bir küre ortalayın. En küçük kürenin hacmi, belirli bir ortalama ile katlanarak dağıtılmalıdır.
9. The squeeze test
1'e ulaşana kadar (0,1) üzerinde rastgele şamandıralarla 2³¹ çarpın. Bunu 100000 kez tekrarlayın. 1'e ulaşmak için gereken şamandıra sayısı belirli bir dağılımı takip etmelidir.
10. Overlapping sums test
(0,1) üzerinde uzun bir rasgele yüzer dizi oluşturun. 100 ardışık float dizisi ekleyin. Toplamlar normalde karakteristik ortalama ve varyansla dağıtılmalıdır.
11. Runs test
(0,1) üzerinde uzun bir rastgele yüzer dizi oluşturur. Artan ve azalan koşuları sayın. Sayılar belirli bir dağılımı izlemelidir.
12. The craps test
Kazançları ve oyun başına atış sayısını sayarak 200000 craps oyunu oynayın. Her sayım belirli bir dağılımı izlemelidir.
Karşılaştırma
Bu bölümde gerçek rastgele sayı üreteçleri ile sözde rastgele sayı üreteçleri karşılaştırılacaktır. Aralarındaki temel farklar tablolar ile gösterilecektir.
- GRSÜ : Gerçek Rastgele Sayı Üreteçleri
- SRSÜ : Sözde Rastgele Sayı Üreteçleri
Aşağıdaki tablo temel karakteristik özelliklerin karşılaştırmasını içerir.
| Karakteristik | SRSÜ | GRSÜ |
|---|---|---|
| Efektiflik | Harika | Zayıf |
| Determinizm | Deterministik | Non-Deterministik |
| Periyodik | Periyodik | Periyodik Değil |
GRSÜ efektiflik olarak zatıftır çünkü üretilmeleri maliyetlidir. SRSÜ ise üretilmeleri kolay olduğundan efektiflikleri yüksektir.
SRSÜ deterministiktir. Yani aynı tohum ile aynı sayı dizisini üretirler. GRSÜ ise fiziki bir dünyadan çok hassas girdi aldıkları için aynı sayı dizisini üretemezler (yani çok zor üretirler).
GRSÜ gerçek manada rastgele sayılar ürettikleri için tekrar içermezler. SRSÜ ise bir periyoda sahiptirler. Yani belli bir miktar sayı ürettikten sonra kullanılan tohum (seed) değerine ulaşırlar. Bu geçen süreye ise periyod denir.
Şimdi ise gerçek rastgele sayı üreteçlerinin kullanım alanlarını inceleyelim.
Aşağıdaki tabloda hangi uygulamalar için hangi üretecin daha uygun olduğu listelenmiştir.
| Uygulama | Hangisi Uygun |
|---|---|
| Çekilişler | GRSÜ |
| Oyunlar | GRSÜ |
| Rasgele örnekleme | GRSÜ |
| Simülasyon ve Modelleme | SRSÜ |
| Güvenlik | GRSÜ |
Çekiliş ve oyunlar gibi gerçek rastgeleliğe ihtiyaç duyulan yerlerde GRSÜ kullanılır. Burada amaç işi gerçek şansa bırakmaktır. Çekilişlerdeki sonuçların bir kurala göre belirlenmesi ve bundan daha da kötüsü bu kuralı bulan birisinin bunu kendi lehine kullanması hiç hoş olmayacaktır.
Similasyon veya test gibi ortamlarda sözde rastgele sayı üreteçleri daha uygundur. Düşük maliyetleri ve performansları ile buradaki ihtiyacı karşılayacaklardır.
Güvenlikte ise tartışmasız bir şekilde GRSÜ kullanılmalıdır. Aksi bir durum kaçınılmaz güvenlik zafiyetlerine neden olacaktır.
Rastgele Yürüyüş (Random Walk) ve Bitmap
Rastgele yürüyüş random sayıları test etmek ve görselleştirmek için kullanılan bir metoddur. Normalde rastgele sayıları matematiksel olarak test etmek oldukça zordur. Bu nedenden dolayı rastgele sayı dizisini görselleştiren metodlar kullanılır. Basit bir görselleştirme ile rastgele sayı üretecinin periyotları ve davranışları çok net bir şekilde görünelibir.
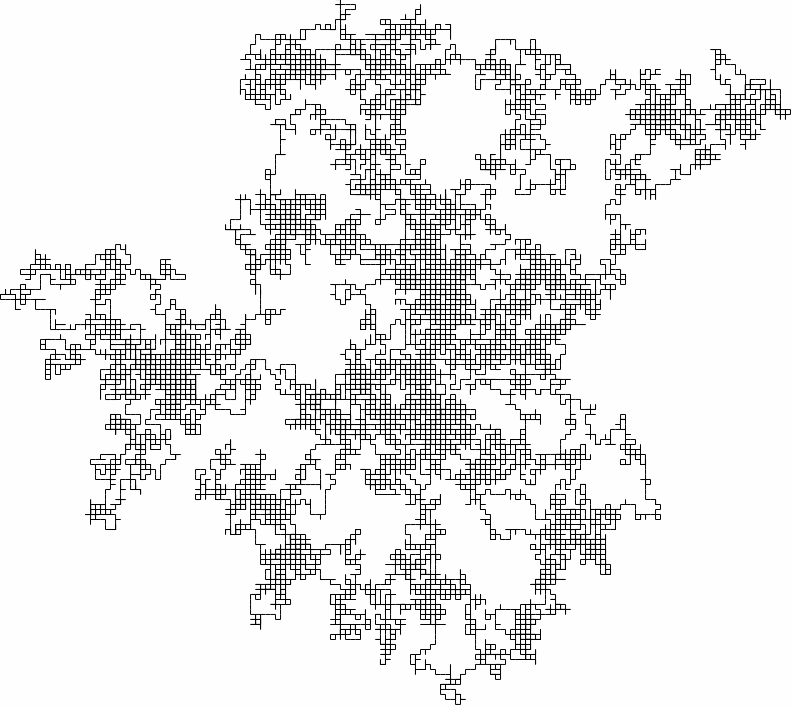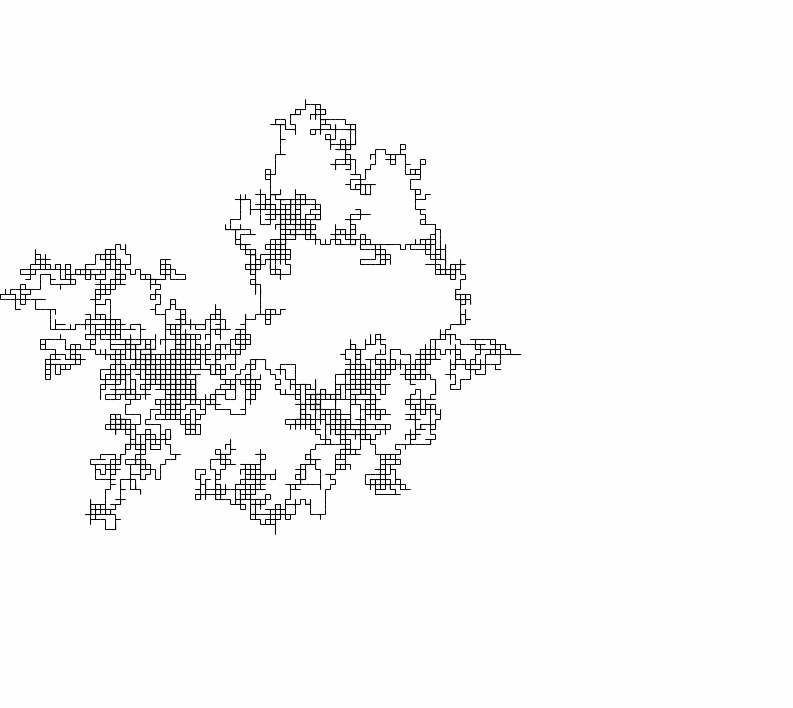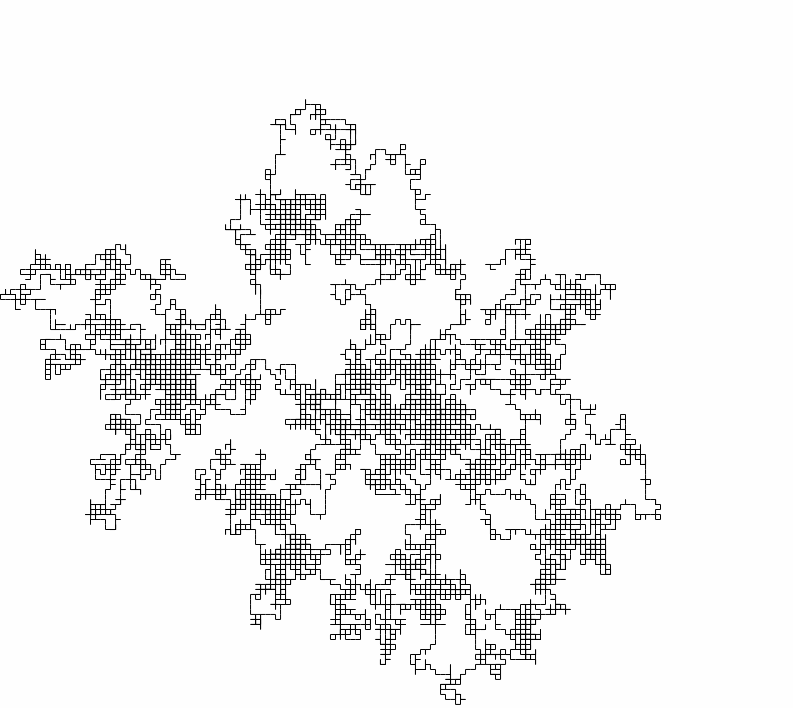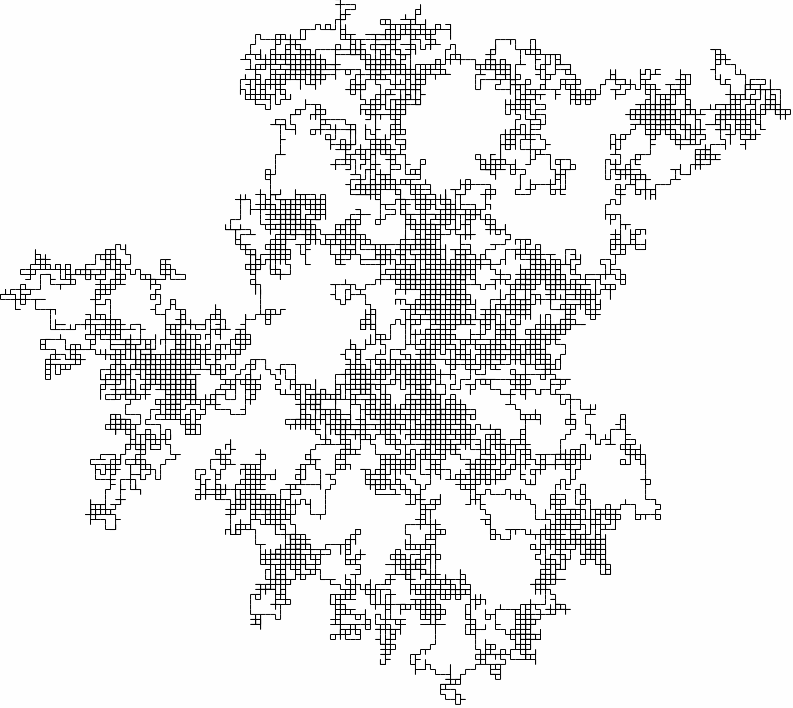
Bir örnek şu şekilde olsun. İnternet üzerinden rastgele sayı üretim hizmeti veren servislerden biri ile üretilen sayılara ait görsel:

Şekilden gördügümüz kadarıyla rastgele bir dağılım var. Herhangi bir desen yada tekrar eden bir şey göre çarpmıyor. Bu gerçek bir rastgele sayı üretecine ait olabilir.
Şimdi diğer örneğe bakalım:

Bu bitmap windows üzerinde çalışan rand() fonksiyonuna ait bir bitmaptir. Görselde göze çarptığı şekilde bir desen ve tekrar eden çizgiler var. İşte bu desen ve desenler arasındaki mesafe bir periyottur. Belirli bir periyot olması demek sayı üretecimizin sözde yani gerçek bir rastgele sayı üreteci olmadığı anlamına gelir.
Başka bir örneğe bakacak olursak şu şekilde bir görsel çıkacaktır.

Burada pembe renkli olan kısım sözde sayı üretecine ait random walk. Beyaz ise gerçek rastgele sayı üretecine ait. Görüldügü üzere belli bir süreden sonra rastgele sayı üreteci tekrar ediyor. [6]
Dünyadan Örnekler
NSA ve Intel Gömülü rastgele sayı üreteci
Geliştiricilerin işlerini kolaylaştırmak ve güvenli rastgele sayılar üretmek için İntel İşlemcileri, RdRand olarak bilinen donanım tabanlı rasgele sayı üreteci barındırırlar. Bu çip, işlemci üzerinde bir entropi kaynağı kullanır ve bir yazılım rastgele sayı talep ettiğinde yazılım için rastgele sayılar üretir.
Buradaki sorun, rastgele sayı üretecinin aslında bir kara kutu olması ve içinde ne olduğunu bilmememiz. RdRand eğer bir NSA arka kapısı içeriyorsa, hükümet yalnızca bu rasgele sayı üreteci tarafından sağlanan verilerle oluşturulan şifreleme anahtarlarını kırabilir.
Bu ciddi bir problem. Aralık 2013'te FreeBSD'nin geliştiricileri, RdRand'ı doğrudan bir rastgele kaynak olarak kullanma desteğini çıkardılar.
RdRand'dan gelen veriler, ek entropi oluşturan başka bir kaynaktan da beslenerek arkakapı olsa bile artık kullanılamayacak bir duruma getiriliyor. Linux uzun zamandır bu şekilde çalışıyordu RdRand'dan gelen verileri ek entropi kaynakları ile besleyerek arkakapı olsa dahi, kullanımını zorlaştırıyordu.
Reddit'teki bir AMA (Ask me anything - Bana Her Şeyi Sor) etkinliğinde, Intel CEO'su Brian Krzanich bu endişelerle ilgili soruları yanıtlamadı ve cevapsız bıraktı.
Hackernews Hacklenmesi
Rastgele sayılardaki bir zafiyetin nelere yol açabileceğini anlamak hackernews platformunun nasıl hacklendiğine bakmak yeterli.
Her ne zaman bir web uygulamasına girdiğinizde size eşsiz bir session id verilir. Bu id tamemen uniq ve başka bir kişi tarafından tahmin edilemez olmalıdır. Eğer bu id başka birileri tarafından tahmin edilebilir yada bulunabilir ise sizi taklit edebilir yada hesabınızı ele geçirebilir.
Hackernews in durumuna baktığımızda session ID'si şuna benzeyen bir değer: "lBGn0tWMcx7380gZyrUO9B". Her giriş yapan kullanıcının buna benzeyen bir ID'si var ve bu değer tahmin edilmesi oldukça zor.
Fakat bu değer gerçek bir rastgele sayı üreteci ile üretilmiyordu. Bunun yerine bir sözde rasgele sayı üreteci kullanılıyordu. Tohum olarak ise hackernews yazılımının başladığı anın milisaniye değeri kullanılıyordu. İşte zafiyet tamda buradaydı.
Dikkatli bir çalışma sonucunda, saldırgan Hacker News'in çökmesini sağladı ve yaklaşık bir dakikalık bir sürede ne zaman yeniden başlatılacağını tahmin edebildi. Ondan sonra, kullanıcılara giriş yaptıkları gibi atanan benzersiz ID'leri tahmin edebildi ve bu nedenle onları taklit edebildi.
Saldırı başarılı oldu çünkü Hacker News yazılımı sunucu çöktükten 1-2 dakika içinde yaniden başlıyordu. Saldırgan yazılımın çöküğü anı ve yeniden başladığı anı not aldıktan sonra bütün kombinasyonları bruteforce ile denedi. Bu iki süre arasında yaklaşık 60.000 kombinasyon olacağı için rastgele sayı üretecinde kullanılan tohum kolay bir şekilde bulundu. [7] [8]
Hacker News yazılımı /dev/urandom aygıtı kullanılmak üzare değiştirildi. Bu aygıt linux sistemlerde gerçek rastgele sayı üretmek üreze kullanılıyor. Yani yeni yazılımla beraber gerçekten random sayılar kullanılarak zafiyet giderildi.
GPG İle Anahtar Üretilmesi
Gpg asimetriş şifreleme için anahtar üreten güçlü bir programdır. Bu program anahtar üretimi sırasında elbette rastgele sayılara ihtiyaç duyar. Bu rastgele sayıları elde etmek için çeşitli kaynaklar kullanır.
Örnek bir anahtar üretimi şu şekildedir.
$ gpg --gen-key
gpg (GnuPG) 2.2.19; Copyright (C) 2019 Free Software Foundation, Inc.
This is free software: you are free to change and redistribute it.
There is NO WARRANTY, to the extent permitted by law.
Note: Use "gpg --full-generate-key" for a full featured key generation dialog.
GnuPG needs to construct a user ID to identify your key.
Real name: suleyman
Email address: [email protected]
You selected this USER-ID:
"suleyman <[email protected]>"
Change (N)ame, (E)mail, or (O)kay/(Q)uit? o
We need to generate a lot of random bytes. It is a good idea to perform
some other action (type on the keyboard, move the mouse, utilize the
disks) during the prime generation; this gives the random number
generator a better chance to gain enough entropy.
We need to generate a lot of random bytes. It is a good idea to perform
some other action (type on the keyboard, move the mouse, utilize the
disks) during the prime generation; this gives the random number
generator a better chance to gain enough entropy.
gpg: key B654433857D24E34 marked as ultimately trusted
gpg: revocation certificate stored as '/home/hello/.gnupg/openpgp-revocs.d/111592469D850CAAF76D2327B654433857D24E34.rev'
public and secret key created and signed.
pub rsa3072 2020-05-02 [SC] [expires: 2022-05-02]
111592469D850CAAF76D2327B654433857D24E34
uid suleyman <[email protected]>
sub rsa3072 2020-05-02 [E] [expires: 2022-05-02]
Anahtar üretimi sırasında gerekli olan isim ve email alanlarını girdikten sonra gpg'nin anahtar üretimi için rastgele değerlere ihtiyacı olduğunu belirtem şu mesaj ile karşılaşıyoruz. Ben hem ingilizce hemde türkçe çevirisini şu şekilde göstereyim.
We need to generate a lot of random bytes. It is a good idea to perform
some other action (type on the keyboard, move the mouse, utilize the
disks) during the prime generation; this gives the random number
generator a better chance to gain enough entropy.
Çok sayıra rastgele bayt üretmeye ihtiyacımız var.
Asal sayı üretirken rastgele eylemler (kılavyede bir şeyler yazmak,
fare hareketleri, disk işlemleri) gerçekleştirmek iyi bir fikir olur.
Bu eylemler rastgele sayı üretecinin yeterli
entropide sayı üretmesi için iyi bir fırsattır.
Uygulama
Rastgeleliği test etmek için çeşitli test setleri kullanılır. Bunlardan en yaygını NIST testleridir. Github üzerinde https://github.com/stevenang/randomness_testsuite adresinde bulunan araç ile rastgele sayılar üzerinde NIST testlerini uygulayacağız.
Programı açtıktan sonra şu şekilde bir ekran ile karşılaşacağız.
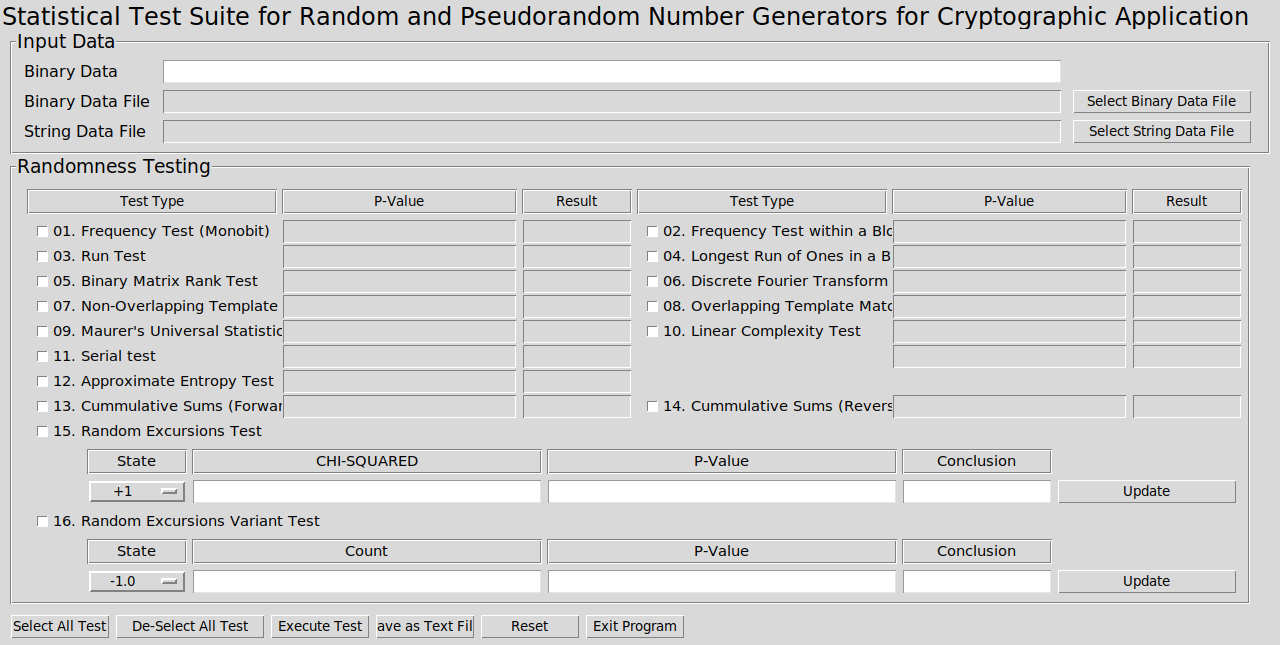
Buradan gerekli sayı dizisini vererek testler gerçekleştirebiliriz.
Öncelikle bizim hem gerçek rastgele sayı üretecinden üretilmiş sayılara hemde sözde rastgele sayı üretecinden üretilmiş sayılara ihtiyacımız var. Bunun için python ile sayı üretiyorum.
from random import random
from os import urandom
from bitstring import BitArray
def sozde():
f = open("sayilar.txt", "w")
for _ in range(100000):
f.write(str(random()) + "\n")
f.close()
def gercek():
f = open("sozde.txt", "w")
for _ in range(100000):
f.write(BitArray(urandom(4)).bin)
f.close()
if __name__=="__main__":
gercek()
sozde()
Öncelikle python da random isimli fonksiyonla sözde rastgele sayılar üretiyorum ve bu sayıları bir dosyaya kaydediyorum.
Aynı şekilde python da os.urandom fonksiyonu ile Linux sistemlerde bulunan ve gerçek tastgele sayı üreten /dev/urandom rastgele sayı alıyorum. Ardından bu sayıları binary formatına dönüştürüp dosyaya kaydediyorum.
Sıra geldi testi başlatmaya. Dosyayı girdi olarak verip testlerimi seçtikten sonra testi başlatıyorum. Ve sonuç şu şekilde
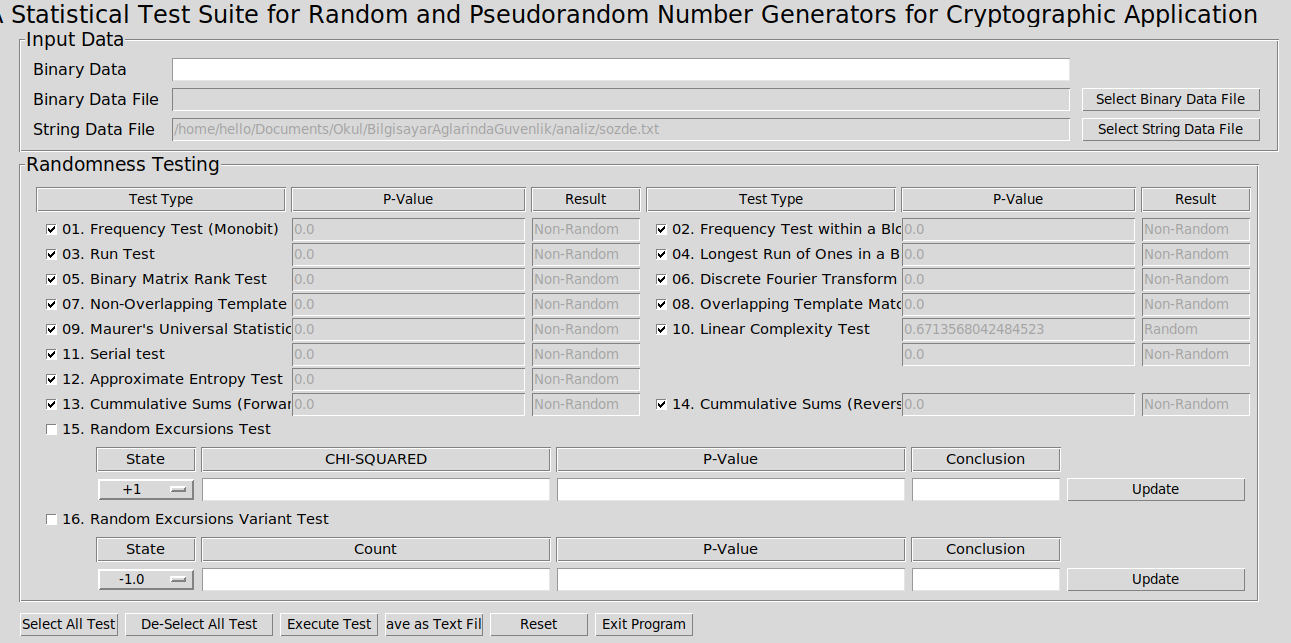
Görüldüğü üzede python da random fonksiyonu ile üretilen sozde.txt dosyasındaki sayılar testleri geçemedi.
Şimdik ise dev/urandom cihazından alınan sayıları test edelim.
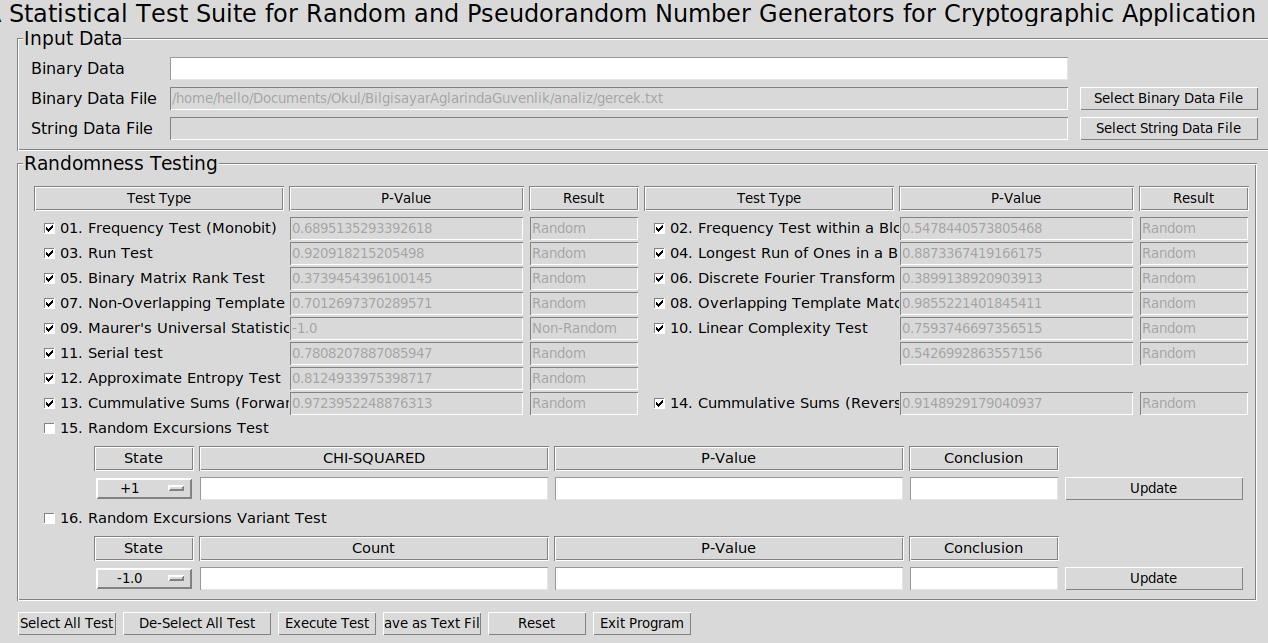
Görüldüğü üzere teslerden başarıyla geçti.
Sonuç
Rastgele sayı üretimi bilgisayar bilimleri açısından oldukça önemlidir. Özellikle kriptoloji alanındaki konumu ile oldukça önemlidir. Şifreleme anahtarlarının üretimi gibi kritik işlemlerde bol miktarda kulanılır. Bu nedenden dolayı rastgele sayı üretimi ciddiye alınmalı ve asla şansa bırakılmamalıdır.
Not
Bu yazıya ilham kaynağı oldukları için Arkakapı Dergisi'ne ve Chris Stephenson'a teşekkürler.
Kaynakça
- [1] https://tr.wikipedia.org/wiki/HTTPS
- [2] Arka kapı dergisi 6. sayı Rastgele sayılar Rastgele Olmayınca Chris Stephenson
- [3] https://bugs.debian.org/cgi-bin/bugreport.cgi?bug=363516
- [4] http://static.dergipark.org.tr/article-download/bef4/cdb8/b1d1/5c876853a73ce.pdf
- [5] https://csrc.nist.gov/projects/random-bit-generation/documentation-and-software/guide-to-the-statistical-tests
- [6] https://tr.khanacademy.org/computing/computer-science/cryptography/crypt/v/random-vs-pseudorandom-number-generators
- [7] https://blog.cloudflare.com/why-randomness-matters/
- [8] https://news.ycombinator.com/item?id=639976
- [9] https://tr.wikipedia.org/wiki/Gerçek_rassal_sayı_üreteci
- [10] http://www.emo.org.tr/ekler/3e6f423ffcbf723_ek.pdf
- https://tr.qwe.wiki/wiki/Random_number_generation
- http://www.emo.org.tr/ekler/3e6f423ffcbf723_ek.pdf
- https://www.iscturkey.org/assets/files/2016/03/2013-paper55.pdf